Linear Elasticity

Linear Elasticity#

Authors:

This notebook serves as a tutorial to solve a problem of linear elasticity using DOLFINx (FEniCS).

You can find a tutorial and useful resources for DOLFINx at the following links

We consider an elastic slab \(\Omega\) with a straight crack \(\Gamma\) subject to a mode-I loading by an applied traction force \(f\), see figure.

Using the symmetry, we will consider only half of the domain in the computation.

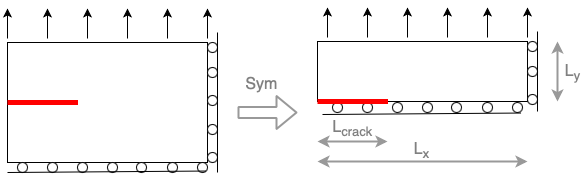
title

We solve the problem of linear elasticity with the finite element method, implemented using DOLFINx.

DOLFINx is advanced library that allows for efficient parallel computation. For the sake of simplicity, we assume here to work on a single processor and will not use MPI-related commands. Using DOLFINx with MPI will be covered in the afternoon session.

We start importing the required libraries.

# Import required libraries
import matplotlib.pyplot as plt
import numpy as np

import dolfinx.fem as fem
import dolfinx.mesh as mesh
import dolfinx.io as io
import dolfinx.plot as plot
import dolfinx.fem.petsc
import ufl

from mpi4py import MPI
from petsc4py.PETSc import ScalarType

Let us generate a mesh using gmsh (http://gmsh.info/). The mesh is refined around the crack tip. The function to generate the mesh is reported in the external file meshes.py located in the directory python. To import it, we add python to the path where the system is looking for functions to import

import sys
sys.path.append("../utils")
from meshes import generate_mesh_with_crack

Lx = 1.
Ly = 0.5
Lcrack = 0.3
lc =.05
dist_min = .1
dist_max = .3
msh, mt, ft = generate_mesh_with_crack(
        Lcrack=Lcrack,
        Ly=Ly,
        lc=lc,  # caracteristic length of the mesh
        refinement_ratio=10,  # how much it is refined at the tip zone
        dist_min=dist_min,  # radius of tip zone
        dist_max=dist_max,  # radius of the transition zone
        verbosity=1
    )

To plot the mesh we use pyvista see:

import pyvista
pyvista.start_xvfb(wait=0.1)
pyvista.set_jupyter_backend("static")
grid = pyvista.UnstructuredGrid(*plot.vtk_mesh(msh))
plotter = pyvista.Plotter()
plotter.add_mesh(grid, show_edges=True)
plotter.camera_position = 'xy'
if not pyvista.OFF_SCREEN:
    plotter.show()
../../_images/20d8d9039d3829aa1cb4ee695b92fea7c2ac0fd8175fa7c79f7ab9d7756e1778.png

Finite element function space#

We use here linear Lagrange triangle elements

V = fem.functionspace(msh, ("Lagrange", 1, (2,)))

Dirichlet boundary conditions#

We define below the functions to impose the Dirichlet boundary conditions.

In our case we want to

  • block the vertical component \(u_1\) of the displacement on the part of the bottom boundary without crack

  • block the horizontal component \(u_0\) on the right boundary

We first get the facets to block on the boundary (dolfinx.mesh.locate_entities_boundary) and then the corresponding dofs (dolfinx.fem.locate_dofs_topological)

def bottom_no_crack(x):
    return np.logical_and(np.isclose(x[1], 0.0), 
                          x[0] > Lcrack)

def right(x):
    return np.isclose(x[0], Lx)

def top(x):
    return np.isclose(x[1], Ly)

delta = 1.0
top_facets = mesh.locate_entities_boundary(msh, msh.topology.dim-1, top)
top_dofs = fem.locate_dofs_topological(V, msh.topology.dim-1, top_facets)
bc_top = fem.dirichletbc(np.array([0.0,delta],dtype=np.float64), top_dofs, V)

right_facets = mesh.locate_entities_boundary(msh, msh.topology.dim-1, right)
right_dofs_x = fem.locate_dofs_topological(V.sub(0), msh.topology.dim-1, right_facets)
bc_right = fem.dirichletbc(np.array(0.0,dtype=np.float64), right_dofs_x, V.sub(0))

# locate the facets of the mesh that are on the bottom boundary and not on the crack
# get the corresponding dofs and define the bc object
bottom_no_crack_facets = mesh.locate_entities_boundary(msh, msh.topology.dim-1, bottom_no_crack)
bottom_no_crack_dofs_y = fem.locate_dofs_topological(V.sub(1), msh.topology.dim-1, bottom_no_crack_facets)
bc_bottom = fem.dirichletbc(0.0, bottom_no_crack_dofs_y, V.sub(1))

# collect the bcs in a list
bcs = [bc_bottom, bc_right]

Define the bulk and surface mesures#

The bulk (dx) and surface (ds) measures are used by ufl to write variational form with integral over the domain or the boundary, respectively.

In this example the surface measure ds includes tags to specify Neumann bcs: ds(1) will mean the integral on the top boundary.

dx = ufl.Measure("dx",domain=msh)
top_facets = mesh.locate_entities_boundary(msh, 1, lambda x : np.isclose(x[1], Ly))
# mt = mesh.meshtags(msh, 1, top_facets, 1) is failing for some installations
# Use then workaround below
mt = mesh.meshtags(msh, 1, top_facets, 1)
ds = ufl.Measure("ds", subdomain_data=mt)

Define the variational problem#

We specify the problem to solve though the weak formulation written in the ufl syntax by giving the bilinear \(a(u,v)\) and linear forms \(L(v)\) in the weak formulation:

find the trial function \(u\) such that for all test function \(v\) \(a(u,v)=L(v)\) with

\[ a(u,v)=\int_{\Omega\setminus\Gamma}\sigma(\varepsilon(u))\cdot \varepsilon(v)\,\mathrm{d}x, \quad L(v)=\int_\Omega b\cdot v \,\mathrm{d}x + \int_{\partial_N\Omega} f\cdot v \,\mathrm{d}s \]

Note on UFL terminology:

  • ufl.inner(sigma(eps(u)), eps(v)) is an expression

  • ufl.inner(sigma(eps(u)), eps(v)) * dx is a form

u = ufl.TrialFunction(V)
v = ufl.TestFunction(V)

E = 1. 
nu = 0.3 
mu = E / (2.0 * (1.0 + nu))
lmbda = E * nu / ((1.0 + nu) * (1.0 - 2.0 * nu))
# this is for plane-stress
lmbda = 2 * mu * lmbda / ( lmbda + 2 * mu )

def eps(u):
    """Strain"""
    return ufl.sym(ufl.grad(u))

def sigma(eps):
    """Stress"""
    return 2.0 * mu * eps + lmbda * ufl.tr(eps) * ufl.Identity(2)

def a(u,v):
    """The bilinear form of the weak formulation"""
    return ufl.inner(sigma(eps(u)), eps(v)) * dx 

def L(v): 
    """The linear form of the weak formulation"""
    # Volume force
    b = fem.Constant(msh,(0.0, 0.0))

    # Surface force on the top
    f = fem.Constant(msh,(1.0, 0.0))
    return ufl.dot(b, v) * dx + ufl.dot(f, v) * ds(1)

Let us plot the solution using pyvista, see

Define the linear problem and solve#

We solve the problem using a direct solver. The class dolfinx.fem.LinearProblem assemble the stiffness matrix and load vector, apply the boundary conditions, and solve the linear system.

problem = fem.petsc.LinearProblem(a(u,v), L(v), bcs=bcs, 
                                    petsc_options={"ksp_type": "preonly", "pc_type": "lu"})
uh = problem.solve()
uh.name = "displacement"

Postprocessing#

We can easily calculate the potential energy

energy = fem.assemble_scalar(fem.form(0.5 * a(uh, uh) - L(uh)))
print(f"The potential energy is {energy:2.3e}")

The potential energy is -7.577e-01

We can save the results to a file, that we can open with paraview (https://www.paraview.org/)

with io.XDMFFile(MPI.COMM_WORLD, "output/elasticity-demo.xdmf", "w") as file:
    file.write_mesh(uh.function_space.mesh)
    file.write_function(uh)

Stress computation#

We calculate here the Von Mises stress by interpolating the corresponding ufl expression, see https://jorgensd.github.io/dolfinx-tutorial/chapter2/linearelasticity_code.html#stress-computation

sigma_iso = 1./3*ufl.tr(sigma(eps(uh)))*ufl.Identity(len(uh))
sigma_dev =  sigma(eps(uh)) - sigma_iso
von_Mises = ufl.sqrt(3./2*ufl.inner(sigma_dev, sigma_dev))
V_von_mises = fem.functionspace(msh, ("DG", 0, (1,)))
stress_expr = fem.Expression(von_Mises, V_von_mises.element.interpolation_points())
vm_stress = fem.Function(V_von_mises)
vm_stress.interpolate(stress_expr)

from plots import warp_plot_2d
plotter = warp_plot_2d(uh,cell_field=vm_stress,
                       field_name="Von Mises stress",
                       factor=0.1,
                       show_edges=False,
                       clim=[0, 4.0])

if not pyvista.OFF_SCREEN:
    plotter.show()
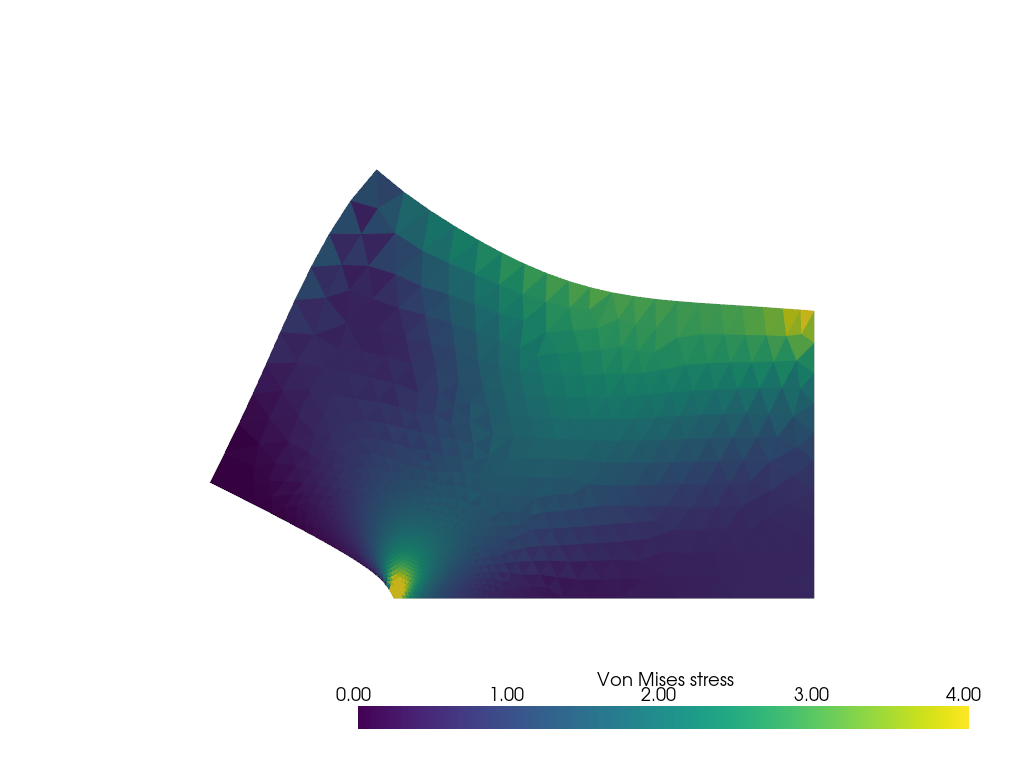
../../_images/47e16f1827abf256bfd205a94797fc7d6958db8aa706dfe42f61aaf11f9713a5.png

We can now wrap all the code in a the external module, so that we can resuse the solver later

We define in elastic_solver.py a function solve_elasticity taking as input the crack length Lcrack, the geoemtric and mesh parameters, the Poisson ratio nu, and giving us as output the solution field uh and the related potential energy energy

The returned uh and energy will be calculated assuming a force density f=1 on the top surface and a Young modulus E=1. This is without loss of generality, see the exercise below.

Exercise.

Let be \(u^{*}\) and \(P^{*}\) the displacement field obtained on a domain \(\Omega^*=[0,1]\times[0,\varrho]\) for a Young module \(E^*=1\) and a load \(f^*=1\) applied on the top surface. Determine by dimensional analysis the analytical formulas giving the displacement \(u\) and the potential energy \(P\) for any other value of \(E\), load \(f\), and for any domain \(\Omega=[0,L]\times[0,\varrho\, L]\) obtained by a rescaling of \(\Omega^*\) with a length-scale \(L\). Deduce that we can, without loss of generality, perform computation with \(E=1\), \(f=1\) and \(L=1\).

from mpi4py import MPI
from elastic_solver import solve_elasticity

uh, energy, _ = solve_elasticity(
    nu=0.3,
    E=1,
    load=1,
    Lx=1,
    Ly=0.5,
    Lcrack=0.3,
    lc=0.1,
    refinement_ratio=10,
    dist_min=0.2,
    dist_max=0.3,
    verbosity=1
)

with io.XDMFFile(MPI.COMM_WORLD, "output/elasticity-demo.xdmf", "w") as file:
    file.write_mesh(uh.function_space.mesh)
    file.write_function(uh)

The potential energy for Lcrack=3.000e-01 is -4.174e-01